Flatiron Internal Conference: Flatiron-wide Algorithms and Mathematics

Oct 30, 2019, 8:15 AM → Nov 1, 2019, 5:00 PM America/New_York

2nd Floor (Ingrid Daubechies Auditorium)

Alex Barnett

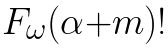
Flatiron-wide Algorithms and Mathematics (FWAM) is a 2.5 day internal conference with the goal of overviewing/introducing a range of numerical algorithms and tools that are essential to research done at Flatiron and beyond. We also aim to form research connections across (and within) the centers, and showcase some of the research which makes use of these methods. Topics have been chosen that are crucial to two or more centers. There are five half-day topics; each begins with at least one accessible, practical, introductory lecture, then short talks that may teach sub-topics or applications to research.

 

Organization team:

Admin: Marian Jakubiak         SCC: Andras Pataki, Pat Gunn

CCA: Gabriella Contardo, Keaton Burns, Dan Foreman-Mackey

CCB: Mike Shelley, Mariano Gabitto

CCM: Manas Rachh, Alex Barnett

CCQ: Olivier Parcollet, Guiseppe Carleo

Wrangler-in-chief: Alex Barnett

 

Session chairs:

Wed am: Alex Barnett / Wed pm: Dan Foreman-Mackey

Thurs am: Olivier Parcollet / Thurs pm: Mike Shelley

Fri am: Gabriella Contardo

 

ZOOM DETAILS IF JOINING REMOTELY:

Join from PC, Mac, Linux, iOS or Android: https://simonsfoundation.zoom.us/j/536451221

Or Telephone:
    Dial(for higher quality, dial a number based on your current location):
        US: +1 646 558 8656  or +1 669 900 6833
    Meeting ID: 536 451 221
    International numbers available: https://zoom.us/u/ahu1dujLA

Wednesday, October 30

8:15 AM Breakfast

Welcome

Optimization Introductory Lecture 1

1 Optimization landscapes - a gentle multi-disciplinary introduction to optimization

In this lecture, I will give an introduction to the field of continuous optimization. I will emphasize instances of optimization problems that appear in biology and physics through the concept of optimization landscapes. I will review sampling-based approaches as well as gradient-based methods and focus on concepts rather than derivations of specific algorithms. The lecture is intended to set the stage for the latter focused talks, and will provide links to other topics covered in the FWAM conference.

Speaker: Christian L. Mueller (CCM / LMU)

FlatironConference2019.pdf

Break

Optimization Introductory Lecture 2

2 Tutorial: Optimization for Machine Learning

A 1-hour version of the MLSS Buenos Aires tutorial notes, focusing on parts 1 and 4, available at the links below.

Speaker: Elad Hazan (Princeton U)

Berkeley lectures youtube, pt 1

Berkeley lectures youtube, pt 2

Boyd & Vandenberghe online book

Elad Hazan's webpage

Lecture notes on optimization for machine learning

MLSS Tutorial notes (parts 1 and 4 were covered at Flatiron)

Break

Optimization Short Talk

3 A practical introduction to adjoint methods

Speaker: Leslie Greengard (CCM / NYU)

adjoint_methods.pdf

4 Research Applications of Optimization: Data-Driven Spectroscopy

Speaker: Megan Bedell (CCA)

FWAM2019-Bedell.pptx

12:30 PM Lunch-

Function Approximation and Differential Equations Introductory Lecture

5 Introduction to interpolation, integration and spectral methods

I overview key concepts and practical methods for efficient and accurate numerical function approximation, integration and differentiation. This is the basis for spectral and other ODE/PDE solvers coming up in the next talk. I will teach concepts such as convergence rate, local/global, adaptivity, rounding error, polynomial and Fourier bases. The focus is on 1D, with pointers to higher-dimensional methods and codes.

Lecture notes (see Lecture I) and codes for demo figures at:
https://github.com/ahbarnett/fwam-numpde

Speaker: Alex Barnett (CCM)

numpde_handout.pdf

Break

Function Approximation and Differential Equations Introductory Lecture

6 Overview of various methods to solve differential equations

We overview various numerical methods to solve ODEs and PDEs.

For source of notes see: https://github.com/ahbarnett/fwam-numpde

Speaker: Keaton Burns (MIT / CCA)

See Lecture II in our notes

Break

Function Approximation and Differential Equations Equations Short Talk

7 PDEs: The long and the short.

Speaker: Michael Shelley (CCB)

8 Introduction to Integral Equation Methods

Speaker: Jun Wang (CCM)

bie_fwam.pdf

9 Wavelets

Speaker: Joakim Andén (CCM)

5:15 PM Reception

Thursday, October 31

8:15 AM Breakfast

Sampling Introductory Lecture

10 Introduction to Markov chain Monte Carlo

Speaker: Dan Foreman-Mackey (CCA)

Break

Sampling Introductory Lecture

11 Scalable Bayesian Inference.

In this short tutorial, I will review variational inference (VI), a method to approximate posterior probability distributions through optimization. VI became popular as it provides faster convergence than more traditional sampling methods.

This tutorial aims to provide both an introduction and an overview of recent developments. First, I will provide a review of variational inference. Second, I describe some popular advancements such as stochastic variational inference, and variational autoencoders. During the talk, I will establish some connections with mathematical problems in different centers at Flatiron.

Speaker: Mariano Gabitto (CCB)

Break

Sampling Short Talk

12 The quantum-ness in quantum Monte Carlo: mathematical and algorithmic implications

Speaker: Prof. Shiwei Zhang (CCQ)

Sampling Short Talk

13 Hierarchical Modeling and Stellar Velocities

An introduction to Bayesian hierarchical modeling, with an example from my own research modeling repeated velocity measurements of distant stars in the Milky Way.

Speaker: Emily Cunningham (CCA)

12:10 PM Lunch

Deep Learning Introductory Lecture

14 Introduction to Deep Learning

A Deep Learning 101 to get familiar with machine/deep learning principles, neural networks, back-propagation, convolution nets and representation learning.

Speaker: Gabriella Contardo (CCA)

DeepLearning_101_FWAM.pdf

Break

Deep Learning Introductory Lecture

15 Introduction to Deep Learning

We will introduce state of the art deep learning methods and showcase some of its applications to astrophysical challenges.

Speaker: Shirley Ho (CCA)

Break

Deep Learning Short Talks

16 Uncertainty Estimation with Neural Networks

Speaker: Laurence Levasseur (CCA / U. de Montreal)

Perreault-Levasseur_FWAM.pdf

17 Deep Generative Modeling for Statistical and Quantum Physics

Speaker: Giuseppe Carleo (CCQ)

18 Biological neural network algorithms

Although traditional artificial neural networks were inspired by the brain they resemble biological neural networks only superficially. Successful machine learning algorithms like backpropagation violate fundamental biophysical observations suggesting that the brain employs other algorithms to analyze high-dimensional datasets streamed by our sensory organs. We have been developing neuroscience-based machine learning by deriving algorithms and neural networks from objective functions based on the principle of similarity preservation. Similarity-based neural networks rely exclusively on biologically plausible local learning rules and solve important unsupervised learning tasks such as dimensionality reduction, clustering and manifold learning. In addition, to modeling biological networks, similarity-based algorithms are competitive for Big Data applications. For further information please see http://www.offconvex.org/2018/12/03/MityaNN2/

Speaker: Mitya Chklovskii (CCB)

5:15 PM Reception

Friday, November 1

8:30 AM Breakfast

Dimension Reduction and Factorization Short Talk

19 Randomized linear algebra and matrix approximation

The goal of this talk is to show how probabilistic methods can be used to accelerate standard matrix factorizations (e.g. SVD) with provable characteristics in terms of speed and accuracy.

Speaker: Eftychios Pnevmatikakis (CCM)

0909.4061.pdf

1505.04650.pdf

main.pdf

woodruff.pdf

20 Spectral Clustering and Dimensionality Reduction

Speaker: Marina Spivak (CCM)

21 Clustering in low dimensions

I will focus on clustering data points in low dimensions (mostly 2d) and provide an overview of some popular clustering algorithms.

The accompanying live notebook is linked from my homepage: https://users.flatironinstitute.org/~magland

Speaker: Jeremy Magland (CCM)

FWAM-clustering-2019 (1).pdf

Break

Dimension Reduction and Factorization Introductory Lecture

22 Fast algorithms for hierarchically structured matrices

In this talk, I will discuss what hierarchically structured matrices are, where they occur in practice, and present algorithms for factorizing these structured matrices. I will demonstrate how the factorization enables subsequent matrix operations (applying the matrix, computing its inverse, and its determinant) in linear CPU time.

Speaker: Manas Rachh (CCM)

pres.pdf

Dimension Reduction and Factorization Short Talk

23 The why and how of nonnegative matrix factorization

Nonnegative matrix factorization (NMF) has become a widely used tool for the analysis of high-dimensional data as it automatically extracts sparse and meaningful features from a set of nonnegative data vectors. I first illustrate this property of NMF on some applications. Then I address the problem of solving NMF, which is NP-hard in general, and review some standard NMF algorithms. Finally, I briefly describe an online NMF algorithm, which scales up gracefully to large data sets.

Speaker: Johannes Friedrich (CCB)

NMF.pdf

24 Introduction to Tensor Network Methods

Tensor network methods are a family of variational algorithms used to simulate many body quantum systems in a variety of situations. With some brief motivation from physics, I'll explain why anyone would want to use these methods, why it is that they are so effective for certain classes of problems, and some extensions to other fields like machine learning.

Speaker: Katharine Hyatt (CCQ)

12:25 PM No Lunch will be served: please order from Seamless