- Indico style
- Indico style - inline minutes
- Indico style - numbered
- Indico style - numbered + minutes
- Indico Weeks View
Flatiron Internal Conference: Flatiron-wide Algorithms and Mathematics
→
America/New_York
2nd Floor (Ingrid Daubechies Auditorium)
2nd Floor
Ingrid Daubechies Auditorium
162 5th avenue, 2nd floor, New York NY, 10010
Description
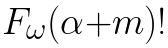
Flatiron-wide Algorithms and Mathematics (FWAM) is a 2.5 day internal conference with the goal of overviewing/introducing a range of numerical algorithms and tools that are essential to research done at Flatiron and beyond. We also aim to form research connections across (and within) the centers, and showcase some of the research which makes use of these methods. Topics have been chosen that are crucial to two or more centers. There are five half-day topics; each begins with at least one accessible, practical, introductory lecture, then short talks that may teach sub-topics or applications to research.
Organization team:
Admin: Marian Jakubiak SCC: Andras Pataki, Pat Gunn
CCA: Gabriella Contardo, Keaton Burns, Dan Foreman-Mackey
CCB: Mike Shelley, Mariano Gabitto
CCM: Manas Rachh, Alex Barnett
CCQ: Olivier Parcollet, Guiseppe Carleo
Wrangler-in-chief: Alex Barnett
Session chairs:
Wed am: Alex Barnett / Wed pm: Dan Foreman-Mackey
Thurs am: Olivier Parcollet / Thurs pm: Mike Shelley
Fri am: Gabriella Contardo
ZOOM DETAILS IF JOINING REMOTELY:
Join from PC, Mac, Linux, iOS or Android: https://simonsfoundation.zoom.us/j/536451221
Or Telephone:
Dial(for higher quality, dial a number based on your current location):
US: +1 646 558 8656 or +1 669 900 6833
Meeting ID: 536 451 221
International numbers available: https://zoom.us/u/ahu1dujLA
Marian Jakubiak
